统计套利交易系统模型
无风险套利机会可以说是很多投资者,特别是量化投资者梦寐以求的,但只要这个市场是个自由的市场,那么可行的无风险套利机会难以长期存在。
而且即使存在着无风险套利机会,其套利收益率也会非常微薄,并不足以能使从事无风险套利交易成为一个值得长期持续的工作,当然,并不能否认市场有时候的确会出现一些长期存在、并且利润丰厚的套利交易机会,市场出现错误的时候。
在量化投资领域,既然严格的无风险套利机会少、收益率微薄,实际的执行过程中也不能完全消除风险。那么如果有一种选择,能够稍微放松100%无风险的要求,比如允许有5%的风险,但同时却能够让套利机会增加100%以上,那岂不是一个更好的选择?
01
统计套利交易模型
1、定义
统计套利交易是指,在量化投资领域,将套利建立在对历史数据进行统计分析的基础之上,估计相关变量的概率分布,并结合基本面数据进行分析以用以指导套利交易。相比于无风险套利,统计套利少量增加了一些风险,但是由此可获得的套利机会将数倍于无风险套利。
2、统计套利的基本思路
统计套利的基本思路是运用统计分析工具对一组相关联的价格之间的关系的历史数据进行研究分析,研究该关系在历史上的稳定性,并估计其概率分布,确定该分布中的极端区域,即否定域,当真实市场上的价格关系进入否定域时,则认为该种价格关系不可长久维持,套利者有较高成功概率进场套利。
如下图所示:
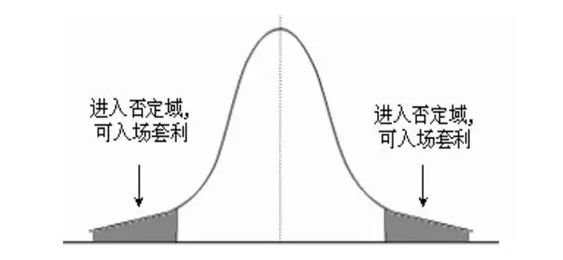
注意:在量化投资领域,统计套利是只针对有稳定性的价格关系进行的,那些没有稳定性的价格关系的套利风险是很大的。价格关系是否稳定直接决定着统计套利能否成立,因此在对价格关系的历史数据进行统计分析的时候,首先要检验价格关系在历史数据中是否稳定。
一组价格关系如果是稳定的,那么必定是存在着某一种均衡关系维持机制,一旦价格关系偏离均衡水平,维持机制就会起作用,将价格关系或快或慢地拉回到均衡水平。
所以,要分析一组价格关系是否稳定,需要先定性分析是否存在着这样的均衡关系维持机制,然后再对历史数据进行统计分析进行验证,以证实该通过定性分析得到的关系维持机制在历史上确实是在发挥作用。
例如:大豆、豆粕、豆油之间的跨品种套利,豆粕与豆油同属于大豆的下游产品,通过之一关系决定了三者之间的均衡关系,通过分析CBOT大豆、豆油和豆粕在过去二十年的历史比价数据,则会发现它们之间的价格关系有很强的稳定性。
国内三大植物油,同属于食用油系列,三者互为替代品,从用途上相互作用,存在均衡的价差关系。通过长期统计分析比价关系比较均衡。
大豆与玉米在种植上属于同一季节作物,在下游又都可以作为饲料的原料,又相互替代,由这两种均衡关系维持着相对稳定的比价关系。
再例如铜和铝,调用它们过去二十年的历史价格数据进行统计分析,容易发现它们之间的价差(比价)是不稳定的,所以针对铜和铝的价差进行的套利是是存在很大风险的。
概言之,进行统计套利,首先是要结合定性和定量两个方面的分析来寻找到一种有着均衡维持机制的稳定的价格关系,然后估计相对价格关系的概率分布,对概率分布进行统计检验。这是统计套利的基础。
3、统计套利交易的优势、局限与风险控制
优点1:
统计套利交易是对无风险套利条件的放松,以增加少量的风险来换取更多的套利机会,最大损失远小于预期收益。
毕竟对于财富的增长,风险只是起着阻碍作用,但是没有风险,财富绝不会自动增长。如果稍微多承担一点风险能换来更多的盈利机会,那么这种交换将是值得的。(主要看风险收益比)
优点2:
对于相关联品种各自的价格走势受共同外因的影响,而往往品种本身的因素决定了相对价格(价差或比价)的走势。
对于来自外界的突发性因素对价差影响不大,因此相对价格的走势的分析往往可以忽略外围的不确定性因素,则只需要把品种本身的供求因素即可,其价差走势相对品种走势较容易把握。这也是套利风险相对较小的原因。




